Mi a bináris keresési fa legrosszabb esete és átlagos esete?

Videó: Mi a bináris keresési fa legrosszabb esete és átlagos esete?

2024 Szerző: Lynn Donovan | [email protected]. Utoljára módosítva: 2023-12-15 23:48

Bináris keresőfa

Algoritmus	Átlagos	Legrosszabb esetben
Tér	Tovább)	Tovább)
Keresés	O(log n)	Tovább)
Beszúrás	O(log n)	Tovább)
Töröl	O(log n)	Tovább)

Ezenkívül mi a nagy O legrosszabb eset időbeli összetettsége egy bináris keresőfában?

A rekurzív szerkezete a BST rekurzív algoritmust ad. Keresés a BST van O (h) legrosszabb - ügy futásidő bonyolultság , ahol h a magassága fa . Mivel s bináris keresőfa n csomóponttal minimum O (log n) szintek, ehhez legalább O (log n) összehasonlítások egy adott csomópont megtalálásához.

Másodszor, mekkora az iterációval végzett bináris keresés időbeni összetettsége? Előadása Bináris keresési algoritmus : Ezért, bináris keresési algoritmus időbeli összetettsége értéke O(log₂n) ami nagyon hatékony. Az általa használt segédtér az O(1) for ismétlődő implementáció és O(log₂n) a hívásverem miatti rekurzív megvalósításhoz.

Az is kérdés, hogy mi lenne a legrosszabb időbeli bonyolultság egy elem keresése során egy bináris keresőfában?

Idő összetettsége : Az legrosszabb esetben összetettsége nak,-nek keresés és beszúrási műveletek O(h), ahol h magassága Bináris keresőfa . Ban ben legrosszabb esetben , mi lehet van nak nek gyökértől utazni nak nek a legmélyebb levélcsomópont. Egy ferde magasságú fa lehet lesz n és az idő összetettsége nak,-nek keresés és helyezze be a műveletet lehet O(n) lesz.

Big O a legrosszabb eset?

Tehát a bináris keresésben a legjobb ügy van O (1), átlagos és legrosszabb esetben van O (bejelentkezés). Röviden: nincs ilyen típusú kapcsolat nagy O -ra használják legrosszabb esetben , Theta átlagosan ügy ”. Mindenféle jelölés használható (és néha használatos is), amikor a legjobb, átlagos, ill legrosszabb esetben egy algoritmusról.

Ajánlott:

Hogyan számítja ki a Round Robin az átlagos várakozási időt?

A várakozási időt Gantt-diagram rajzolásával számíthatja ki, így az i-edik folyamat várakozási ideje megegyezik a Befejezési idővel - (Érkezési idő + sorozatfelvételi idő). P1 utolsó indítási ideje 24 (amikor P1 3. alkalommal fut a Gannt-diagramon) P1 2-szer előzve az élettartama során Kvantum = 4, Érkezés = 0

Mi az AWS Storage Gateway fő használati esete?

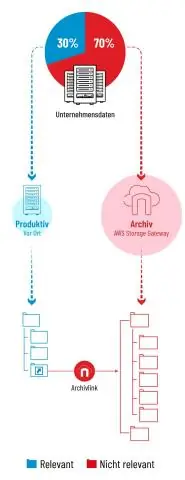
A tipikus használati esetek közé tartozik a biztonsági mentés és az archiválás, a katasztrófa-helyreállítás, az adatok S3-ba való áthelyezése a felhőben történő munkaterheléshez, valamint a többszintű tárolás. Az AWS Storage Gateway három tárolási felületet támogat: fájl, szalag és kötet